Spins with one components: S=±1
Energy=-S.hlocal=-S.h
P(x)=e-Energy/T
=eh.S
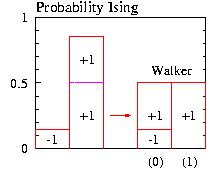
The probability of the Ising states (±1) are shown on the left. On the right the Walker probability.
|
|
|
Spins with one components: S=±1 Energy=-S.hlocal=-S.h P(x)=e-Energy/T =eh.S |

The probability of the Ising states (±1) are shown on the left. On the right the Walker probability. |
|
|
|
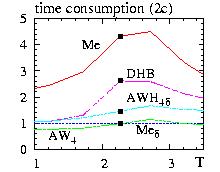
|