The Fast Linear Algorithm
for O(1) symmetry (-1<S<1)



Spins with one components: S=x
local field : hlocal=(hlocalx)
Energy=-S.hlocal=-hlocal.x
P(x)=e-Energy/T.dx
       =eh.x.dx
The Fast Linear Algorithm (FLA) uses the rejection method with a function consisting of n steps (see the figure and article for more details)

Download the Fast Linear Algorithm:
1.  To use the Fast Linear Algorithm you must have :
2.  AND you must have the tables in the file "O1.res". Two choices: . You can choose to download the file O1.res already done or make one with create_O1.out (.exe for windows), run it, and follow the instructions.
  • O1.res   (380 Ko)
    h → [0,100[ with rate=85%
 or
  • For LINUX, only one executable
    create_O1.out   (For LINUX, 450 Ko)
  • For WINDOWS copy these two programs in the same directory
    1. create_O1.exe   (For WINDOWS, 34 Ko)
    2. cygwin1.dll   (For WINDOWS, 950 Ko)

Download the Article:

Probabilities and Performances :
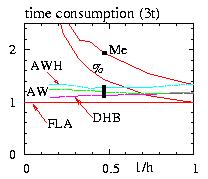
  • Figure: comparison of the time of simulation for various algorithms (Metropolis,Me, Direct Heat Bath, DHB, and Fast Linear Algorithm, FLA) for the two and three dimensional antiferromagnetic triangular lattices (2t and 3t) and the ferromagnetic square lattices (2c)
    The critical temperatures are shown by the squares
    The Fast Linear Algorithm (FLA) is the fastest of all algorithms proposed (2 times faster than the Metropolis Me, at the critical temperature in this case). We can show more generally that another algorithm cannot be faster (see article).
    More...

Other Algorithms in C