The Fast Linear Algorithm
for O(2) symmetry Probabilities and Performances :

The Fast Linear Algorithm is the fastest of all algorithms proposed. Indeed we can show generally that another algorithm cannot be faster (see article).

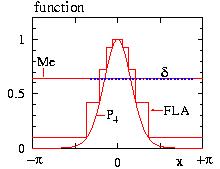
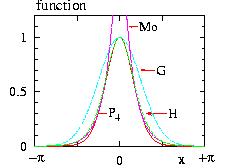
Figure: The probability P(x) and the test function f(x) for various algorithms. FLA=Fast Linear Algorithm AWH=Alias Walker Hasting Me  =Metropolis d    =Metropolis with restriction Mo=Moriarty G  =Gaussian H  =Hattori P4=P(x) with h=4
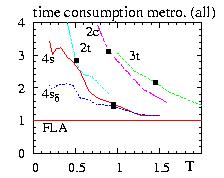
Figure: comparison of the time of simulation for various algorithms and various systems. The critical temperatures are shown by the squares Metropolis/FLA for the: 2c=two dimensional square lattices with ferromagnetic interactions 2t=two dimensional triangular lattices with antiferromagnetic interactions 3t=three dimensional triangular lattices with antiferromagnetic interactions 4s=four dimensional cubic lattices with ± interactions (the exchange MC algorithm is also used)
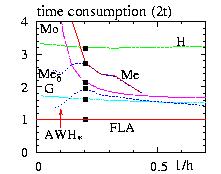
for the 2 dimensional triangular antiferromagnetic system with XY spins. FLA=Fast Linear Algorithm AWH=Alias Walker Hasting Me  =Metropolis d    =Metropolis with restriction Mo=Moriarty G  =Gaussian H  =Hattori
Figure: comparison of the rate of simulation for various algorithms for the 2 dimensional triangular antiferromagnetic system with XY spins. FLA=Fast Linear Algorithm AWH=Alias Walker Hasting Me  =Metropolis d    =Metropolis with restriction Mo=Moriarty G  =Gaussian H  =Hattori The critical temperature is shown by the squares

---

• go to ~loison/fast_algorithms/O2/
• go to ~loison/fast_algorithms/
• go to ~loison/
• mail to D. Loison