The Fast Linear Algorithm
for O(4) symmetry
Probabilities and Performances :

The Fast Linear Algorithm is the fastest of all algorithms proposed. Indeed we can show generally that another algorithm cannot be faster (see article).
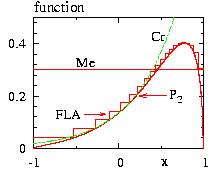
  • Figure: The probability P(x) and the test function f(x) for various algorithms.
    FLA=Fast Linear Algorithm
    Cr  =Creutz
    Me  =Metropolis
    P2=P(x) with h=2
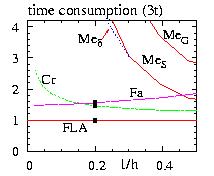
  • Figure: comparison of the time of simulation for various algorithms for the stacked triangular antiferromagnetic lattices.
    The critical temperature is shown by the squares
    • FLA=Fast Linear Algorithm
    • Cr  =Creutz
    • Fa  =Fabricius
    • Ke  =Kennedy
    • MeG =Metropolis standard using 4 Gaussian random numbers.
    • MeS =Metropolis, the first angle, sin2(theta)is chosen from a sinus distribution and the rejection method
    • Med =like MeS but the first angle is constrained to be around the old spin (0 < first angle < d).
  • Figure: comparison of the rate of simulation for various algorithms for the stacked triangular antiferromagnetic lattices.
    The critical temperature is shown by the squares
    • FLA=Fast Linear Algorithm
    • Cr  =Creutz
    • Fa  =Fabricius
    • Ke  =Kennedy
    • Me =Metropolis .
    • Med = Metropolis but the first angle is constrained to be around the old spin (0 < first angle < d).